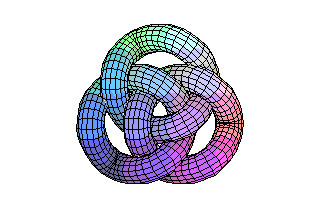TOPOLOGY

Topology is a math discipline who treats of the research of invariants in a geometry cleared of all idea of measurement or of distance. Applied to the learning of surfaces, for example, it studies the invariants who resist to the distortion of these. Of recent apparition (middle of XIXème, Listing, Möbius, etc..), topology abandons all metrics in order to interest of qualitative manner to the spatial relationships between the different parts of figures. Lacan shows that the logic of the unconscious refers to the topology. Starting from 1961, he clings to show the nature topologic of the joint of the principal concepts of the psychoanalysis. Some patterns like the band of Möbius, the torus, the cross-cap, the bottle of Klein or again different types of knots realize respectively for Lacan the constitution of the subject, of some dealings between the ask and the desire, of fantasies, of the nature of the object a ,[etc]. But for the psychoanalysis, topology is not only a pattern: Lacan learn us to consider it like the very structure.

Here are fundamental objects of the lacanian topology :

The Möbius band

The torus

The Klein bottle

The cross-cap

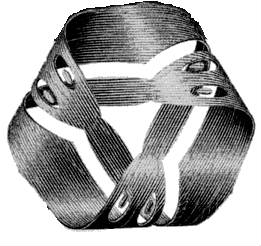
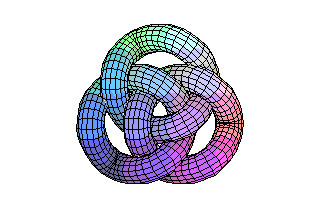The borromean knot

Topology is a branch of pure mathematics, deals with the fundamental properties of abstract spaces. Whereas classical geometry is concerned with measurable quantities, such as angle, distance, area, and so forth, topology is concerned with notations of continuity and relative position. Point-set topology regards geometrical figures as collections of points, with the entire collection often considered a space. Combinatorial or algebraic topology treats geometrical figures as aggregates of smaller building blocks.
BASIC CONCEPTS
In general, topologists study properties of spaces that remain unchanged, no matter how the spaces are bent, stretched, shrunk, or twisted. Such transformations of ideally elastic objects are subject only to the condition that nearby points in one space correspond to nearby points in transformed version of that space. Because allowed deformation can be carried out by manipulating a rubber sheet, topology is sometimes known as rubber-sheet geometry. In contrast, cutting, then gluing together parts of a space is bound to fuse two or more points and to separate points once close together. The basic ideas of topology surfaced in the mid-19th century as offshoots of algebra and ANALYTIC GEOMETRY. Now the field is a major mathematical pursuit, with applications ranging from cosmology and particle physics to the geometrical structure of proteins and other molecules of biological interest.
In essence, the topology of a space provides a way of telling which points are very close to one another and which are not. For instance, it supplies a way of determining whether a curve drawn on a space is continuous (unbroken) or not. However, it does not distinguish between a smooth and crinkly curve or say anything about the curve's length. Topology does not deal with smoothness or size. Hence, a cube's surface has the same topology as a sphere's surface, even though one has sharp corners and the other smooth. Such topologically identical figures are termed homeomorphic. On the other hand, the surface of a sphere has a difficult topology from the surface of a torus (doughnut-shaped space).
A primary aim of topology is to find a serviceable set of rules or procedures for recognizing spaces in all dimensions. In such a classification scheme, two spaces would belong to the same topological class if they had the same basic, overall structure although they might differ drastically in their details.
The simplest topological spaces are known as Euclidean spaces. In general, the term DIMENSION signifies an independent parameter, or coordinate. A space has n dimensions if each of its points is completely determined by n independent numbers. An infinitely long line is a one-dimension Euclidean space. The plane is a two-dimensional Euclidean space. The space of ordinary experience is usually considered a three-dimensional Euclidean space.
MANIFOLDS
The term manifold covers more complicated types than Euclidean spaces. Manifolds locally appear flat, or Euclidean, but on a larger scale may bend and twist into exotic and intricate forms. Any surface, however curved and complicated, so long as it does not intersect itself, can be thought of as consisting of small, two-dimensional, Euclidean patches glued together. Special manifold characteristics, often expressed as numbers or algebraic expressions, help distinguish manifolds. Such expressions, known as topological invariants, provide a convenient way of categorizing manifolds. Dimension, the number of coordinates required to specify a point in a given space, is one example of a topological invariant. Manifolds may also be either bounded or unbounded. A circle is an example of a bounded, one-dimensional manifold, but a line stretching off indefinitely in both directions is unbounded. The same distinction applies to spaces of any dimension. Certain types of two-manifolds, termed compact surfaces, can be classified in terms of an invariant called the Euler number. For a compact surface divided into triangles, the surface's Euler number equals the number of triangles minus the number of edges plus the number of vertices (a vertex is the point of a triangle farthest from its base). No matter how the surface is divided up into triangles--so long as no triangle's vertex rests on another triangle's edge--each different type of compact surface has a particular Euler number. The sphere has Euler number 2; the torus has Euler number 0; the surface of a two-handled soup tureen has a Euler number of -2. Each even integer less than or equal to 2 is the Euler number for exactly one type of closed surface.
The same idea can be expressed in terms of spheres to which are attached a certain number of handles. The surface of a sphere or a lump of clay fall into one group, whereas the surface of a doughnut or a coffee mug fall into another. Because both forms have one hole, one can imagine smoothly deforming a doughnut-shaped piece of clay to produce a mug with a single handle. On the other hand, there is no way, short of cutting, to turn a spherical balloon into an inner tube.
Topologists, using suitable invariations, can examine in detail what manifolds look like and how one can be transformed into another. Much manifold study concerns the search for more finely tuned invariants that make subtler distinctions. Because manifolds in higher dimensions are impossible to visualize, these invariants often stand in for the manifolds.
MANIFOLD CLASSIFICATION
Mathematicians have developed workable schemes for studying manifolds in every dimension except three and four. Dimension three remains a puzzle because proposed classification schemes cover only a portion of all conceivable three-manifolds. Recent attempts to demystify four-dimensional spaces reveal them to have special characteristics quite unlike those of any dimension, higher or lower. The Poincare conjecture, named for the French mathematician Henri POINCARE, ranks as one of the most baffling and challenging unsolved problems in algebraic topology. The central idea of homotopy theory (the theory of the relationship between topologically identical spaces) is to reduce topological questions to abstract algebra by associating with topological spaces various algebraic invariants. Poincare's contribution was the invention of an abstract concept called the fundamental group for distinguishing different categories of two-dimensional surfaces. Poincare was able to show that any two-dimensional surface having the same fundamental group as the two-dimensional surface of a sphere is topologically equivalent to such a sphere. He then conjectured that the same relationship holds for three-dimensional manifolds, and other mathematicians extended the idea to higher dimensions. Ironically, mathematicians have provided the equivalent of Poincare's conjecture for all dimensions except three. The central problem in proving the conjecture in three dimensions is that, unlike the two-manifolds cases, topologists have no complete classification scheme for three-manifolds. There exists no list of all possible manifolds that can be checked one by one to make sure that all have different homotopy groups.
KNOT THEORY
Topology is also concerned with the ways in which one manifold may be embedded within another, such as the ways a knotted circle may be embedded in three-dimensional space. A mathematical knot is the abstract result of first looping and interlacing a piece of string, then joining its ends together. Because any such knot is always topologically equivalent to a circle, the central questions in knot theory concern how that curve is embedded in three-dimensional space.
Knot theorists are particularly interested in identifying when curves are truly knotted, in finding ways of distinguishing different knots, and, more generally, in classifying all possible knots. Although a competent scout or sailor can readily identify and distinguish between a reef knot and a granny knot, mathematicians have a tougher task because they must deal with all conceivable knots. In many cases, two knots may look the same when, in fact, they are different. Alternatively, a knot may be so contorted that its true identity is masked.
To make knot classification easier, investigators examine the two-dimensional shadows cast by the three-dimensional knots. Even the most tangled configuration can be pictured as a continuous loop whose shadow winds across a flat surface, sometimes crossing over, and sometimes crossing under itself. One convenient measure of a knot's complexity is the minimum number of crossings that show up after looking at all possible shadows of a particular knot. A loop without any twists of crossings (in its simplest form, a circle) is called an unknot. The simplest possible knot is the overhand, or trefoil, knot, which is really just a circle that winds through itself. In its plainest form, this knot has three crossings. It also comes in two forms: left-handed and right-handed configurations, which are mirror images of each other. Knot theorists have identified 12,965 distinct knots with 13 or fewer crossings.
A more sophisticated approach to distinguishing knots is to use the arrangement of crossings in a knot diagram to produce an algebraic expression--a polynomial invariant--that serves as a label for the knot. Recent discoveries of a wide range of new invariants show promise because they seem to distinguish more different types of knots than previously known invariants.
Ivars Peterson
Bibliography:
Francis, G. K., A Topological Picturebook (1987); Firby, P, A., and Gardiner, C. F., Surface Topology (1982); Barr, Stephen, Experiments in Topology (1972); Weeks, Jeffrey R., The Shape of Space (1985); Peterson, Ivars, Islands of Truth (1990) and The Mathematical Tourist (1988); Stewart, Ian, The Problem of Mathematics (1987).

go back